Caen, le 1er Août 1881¹
Faculté des sciences de Caen – Instruction Publique

Mon cher ami,

Permettez-moi de vous envoyer encore un exemple relatif à notre équation \[\sum {u_i F_i \frac{dz}{du_i}} = z\] exemple qui mettra bien en lumière la nature et les propriétés de l’intégrale.

Je suppose, vous vous le rappelez, que, quand on annule tous les \(u\), \[F_1 ,\;F_2 ,\quad \ldots \quad F_n \;\] se réduisent à 1, \[x - \alpha_2 ,\quad \ldots \quad x - \alpha_n.\]

Je pose :² \[z = tu_1\] d’où : \[\frac{{dz}} {{du_i }} = u_1 \frac{{dt}} {{du_i }}\quad \quad \frac{{dz}} {{du_1 }} = t + u_1 \frac{{dt}} {{du_1 }}\]

L’équation (1) va devenir, en supposant n = 3 pour fixer les idées : \[u_1 F_1 \frac{{dt}} {{du_1 }} + u_2 F_2 \frac{{dt}} {{du_2 }} + u_3 F_3 \frac{{dt}} {{du_3 }} = t\left( {1 - F_1 } \right)\]

Je pose maintenant : \(t = e^v\) d’où \[\frac{{dt}}{{du_i }} = e^v \frac{{dv}}{{du_i }}\] l’équation (1) devient alors : \[u_1 F_1 \frac{{dv}}{{du_1 }} + u_2 F_2 \frac{{dv}}{{du_2 }} + u_3 F_3 \frac{{dv}}{{du_3 }} = \left( {1 - F_1 } \right)\] ou en posant : \[\frac{{F_2 }} {{F_1 }} = \varphi_2 \quad \frac{{F_3 }} {{F_1 }} = \varphi_3 \quad \frac{{1 - F_1 }} {{F_1 }} = \varphi\] \[u_1 \frac{{dv}} {{du_1 }} + u_2 \varphi_2 \frac{{dv}} {{du_2 }} + u_3 \varphi_3 \frac{{dv}} {{du_3 }} = \varphi\]

Quand on annule tous les u, les fonctions \[\varphi_2 ,\;\varphi_3 \;\text{et}\;\varphi\] se réduisent respectivement à : \[x - \alpha_2 ,\;x - \alpha_3 ,\;0\]

Eh bien, je vais supposer que \[\varphi_2 \;\text{et}\;\varphi_3\] se réduisent identiquement à \[x - \alpha_2 ,\;x - \alpha_3;\] j’aurai ainsi un exemple simple où l’intégrale s’écrira presqu’immédiatement.

Soit en effet : \[\varphi = \sum {A_{m_1 ,\;m_2 ,\;m_3 } } u_1^{m_1 } u_2^{m_2 } u_3^{m_3 }\] et écrivons que la fonction inconnue v s’écrit : \[v = \sum {C_{m_1 ,\;m_2 ,\;m_3 } } u_1^{m_1 } u_2^{m_2 } u_3^{m_3 }\]

On a, en identifiant : \[C_{m_1 ,\;m_2 ,\;m_3 } \left( {m_1 + m_2 \left( {x - \alpha_2 } \right) + m_3 \left( {x - \alpha_3 } \right)} \right) = A_{m_1 ,\;m_2 ,\;m_3 }\] ce qui donne les valeurs des C. Il n’y aurait en effet de difficulté que si l’on avait : \[m_1 + m_2 \left( {x - \alpha_2 } \right) + m_3 \left( {x - \alpha _3 } \right) = 0\]

Or dans le cas où l’origine est extérieure au triangle formé par les points 1, \(x - \alpha_2 ,\;x - \alpha_3\) ; cela ne peut arriver que si³

\[m_1 = m_2 = m_3 = 0.\]

Mais alors, comme \(A_{0,\;0,\;0}\) est nul, l’équation (2) se réduit à une identité.

Quant à la convergence de la série, elle se démontre aisément dans le cas où l’origine est extérieure au triangle \(1, x - \alpha_2 ,\;x - \alpha_3\).⁴

On a donc une fonction v holomorphe définie par la série convergente : \[v = \sum {\frac{{A_{m_1 ,\;m_2 ,\;m_3 } u_1^{m_1 } u_2^{m_2 } u_3^{m_3 } }} {{m_1 + m_2 \left( {x - \alpha_2 } \right) + m_3 \left( {x - \alpha_3 } \right)}}}\] ce qui définit en même temps une intégrale z holomorphe de l’équation (1).

Ces fonctions \(v\) et \(z\) présenteront un espace lacunaire déterminé par la condition que l’origine soit intérieure au triangle \(1,\;x - \alpha_2 ,\;x - \alpha_3\). Cet espace lacunaire est limité par trois droites, dont l’une est la droite \(\alpha_2 \alpha_3\) et les autres sont les parallèles à l’axe des quantités réelles menées par \[\alpha_2 \;\text{et}\;\alpha_3\] dans la direction des quantités réelles négatives.⁵

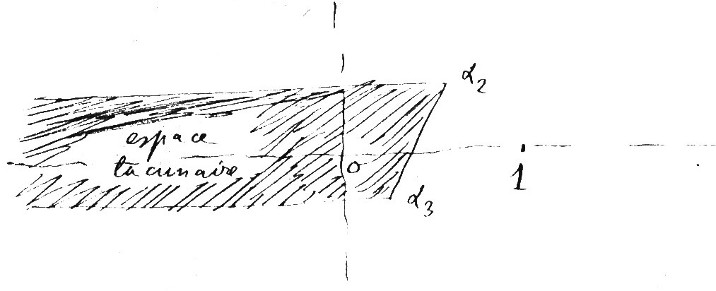
Si au lieu de supposer que \(F_2\) et \(F_3\) se réduisent à \(x - \alpha_2 ,\;x - \alpha_3\) quand on annule tous les \(u\), j’avais supposé que ces fonctions se réduisent à \[\frac{{x - \alpha_2 }} {{x - \alpha_1 }},\quad \frac{{x - \alpha_3 }} {{x - \alpha_1 }}\] j’aurais eu pour espace lacunaire le triangle \(\alpha_1 \alpha_2 \alpha_3\).⁶ Vous voyez comment dans le cas simple où l’on a identiquement : \[F_2 = F_1 \times \left( {x - \alpha_2 } \right)\quad \quad F_3 = F_1 \times \left( {x - \alpha_3 } \right)\] ou bien \[F_2 = F_1 \times \frac{x - \alpha_2} {x - \alpha_1}\quad \quad F_3 = F_1 \times \frac{x - \alpha_3} {x - \alpha_1}\] la question peut se traiter. Si vous le désirez d’ailleurs, je pourrai vous envoyer un exemple plus compliqué.

Veuillez agréer, mon cher ami, l’assurance de mes sentiments les plus dévoués.

Poincaré